Apollonius diagram 简介

Apollonius diagram (or the Additively weighted Voronoi diagram) 其距离函数定义为点到球表面的最短距离（可以是负值，若点在球内）：

$$\delta(x, P_i)=||x-c_i||-w_i$$

其对偶图为 Apollonius graph ，每个面都有三条边（将无穷远点加入 Apollonius diagram 后）。

其区域边界为双曲线一支，或者垂直平分线（当 $w_i=w_j$ 时），当球 $j$ 完全在球 $i$ 内时， $j$ 为隐藏点。

区域有星形性质(Star-shaped)，每个区域 $V_i$ 关于其生成中心 $c_i$ 是星形可见的。这意味着从区域内任意一点 $x$ 到 $c_i$ 的线段全都在 $V_i$ 内部（用三角不等式易证）。这保证了区域的连通性。

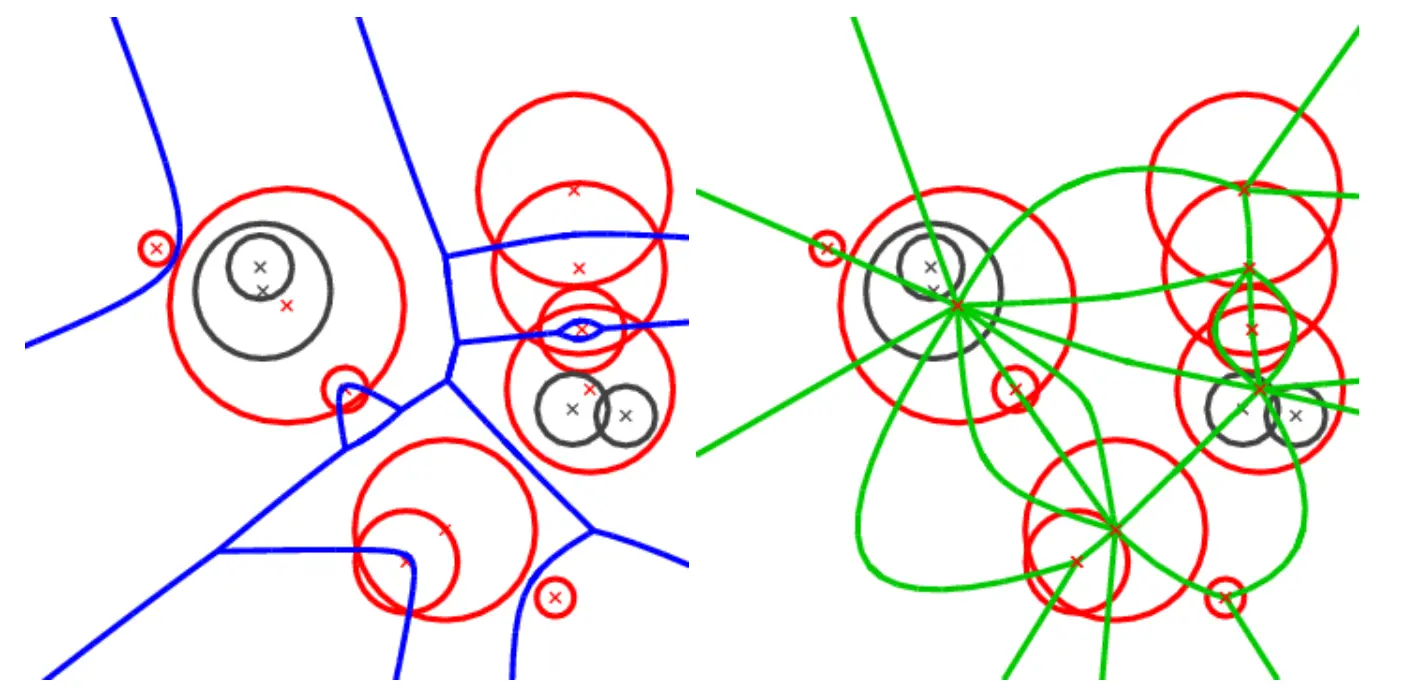
参考

• CGAL 6.1.1 - 2D Apollonius Graphs (Delaunay Graphs of Disks)