梯度上升与朗之万动力学采样

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

# ==========================================
# 1. 定义目标分布 p(x) (双峰高斯)
# ==========================================
def target_pdf(x):
    # 混合两个高斯: 0.7 * N(-2, 1) + 0.3 * N(4, 1.5)
    p1 = 0.7 * np.exp(-0.5 * ((x + 2) / 1)**2) / (np.sqrt(2 * np.pi) * 1)
    p2 = 0.3 * np.exp(-0.5 * ((x - 4) / 1.5)**2) / (np.sqrt(2 * np.pi) * 1.5)
    return p1 + p2

def get_score(x):
    # 计算 Score Function: ∇ log p(x) = p'(x) / p(x)
    # 为了数值稳定，这里显式写出导数
    p = target_pdf(x)
    
    # dp/dx calculation
    grad_p1 = 0.7 * np.exp(-0.5 * ((x + 2) / 1)**2) / (np.sqrt(2 * np.pi) * 1) * (-(x + 2) / 1**2)
    grad_p2 = 0.3 * np.exp(-0.5 * ((x - 4) / 1.5)**2) / (np.sqrt(2 * np.pi) * 1.5) * (-(x - 4) / 1.5**2)
    
    grad_p = grad_p1 + grad_p2
    
    # 避免除以0，加个极小值
    return grad_p / (p + 1e-10)

# ==========================================
# 2. 模拟参数
# ==========================================
n_particles = 2000    # 粒子数量
n_steps = 500         # 迭代步数
tau = 0.1             # 步长 (学习率)
noise_scale = np.sqrt(2 * tau) # 朗之万噪声系数

# 初始化粒子 (均匀分布在区间 [-8, 10])
x_opt = np.random.uniform(-8, 10, n_particles) # 用于优化 (梯度上升)
x_sample = x_opt.copy()                        # 用于采样 (朗之万)

# ==========================================
# 3. 迭代更新
# ==========================================
for t in range(n_steps):
    score_opt = get_score(x_opt)
    score_sample = get_score(x_sample)
    
    # --- 算法 1: 梯度上升 (找极值) ---
    # x = x + τ * ∇log p(x)
    x_opt = x_opt + tau * score_opt
    
    # --- 算法 2: 朗之万动力学 (采样) ---
    # x = x + τ * ∇log p(x) + √(2τ) * z
    noise = np.random.normal(0, 1, n_particles)
    x_sample = x_sample + tau * score_sample + noise_scale * noise

# ==========================================
# 4. 绘图结果
# ==========================================
fig, axes = plt.subplots(1, 2, figsize=(14, 6), sharey=True)
x_grid = np.linspace(-8, 10, 1000)
true_pdf = target_pdf(x_grid)

# --- 左图: 梯度上升 (求极值) ---
axes[0].plot(x_grid, true_pdf, 'r--', label='True p(x)', lw=2)
axes[0].hist(x_opt, bins=50, density=True, color='blue', alpha=0.6, label='Particles')
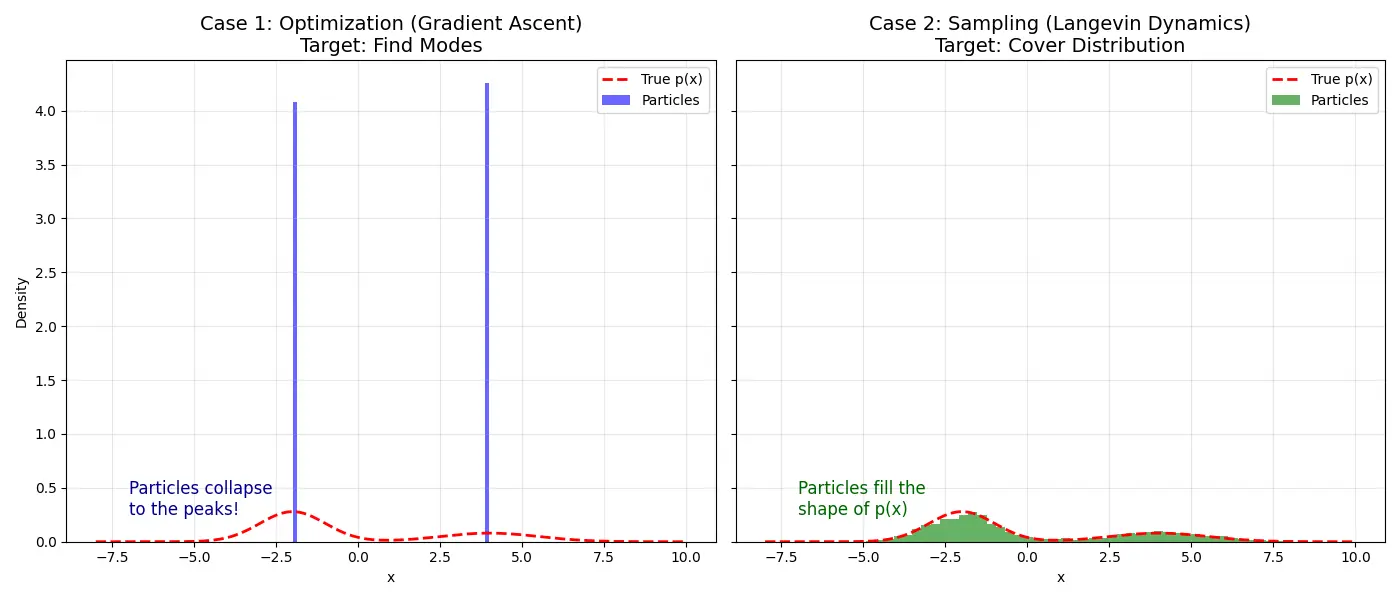
axes[0].set_title('Case 1: Optimization (Gradient Ascent)\nTarget: Find Modes', fontsize=14)
axes[0].set_xlabel('x')
axes[0].set_ylabel('Density')
axes[0].legend()
axes[0].grid(True, alpha=0.3)
axes[0].text(-7, 0.25, "Particles collapse\nto the peaks!", fontsize=12, color='darkblue')

# --- 右图: 朗之万动力学 (采样) ---
axes[1].plot(x_grid, true_pdf, 'r--', label='True p(x)', lw=2)
axes[1].hist(x_sample, bins=50, density=True, color='green', alpha=0.6, label='Particles')
axes[1].set_title('Case 2: Sampling (Langevin Dynamics)\nTarget: Cover Distribution', fontsize=14)
axes[1].set_xlabel('x')
axes[1].legend()
axes[1].grid(True, alpha=0.3)
axes[1].text(-7, 0.25, "Particles fill the\nshape of p(x)", fontsize=12, color='darkgreen')

plt.tight_layout()
plt.show()